题目

给定一段一段的绳子，你需要把它们串成一条绳。每次串连的时候，是把两段绳子对折，再如下图所示套接在一起。这样得到的绳子又被当成是另一段绳子，可以再次对折去跟另一段绳子串连。每次串连后，原来两段绳子的长度就会减半。

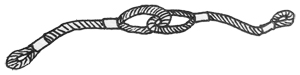
rope.jpg

给定 $N$ 段绳子的长度，你需要找出它们能串成的绳子的最大长度。

输入格式：

每个输入包含 1 个测试用例。每个测试用例第 1 行给出正整数 $N$ ( $2 \le N \le 10^4$ )；第 2 行给出 $N$ 个正整数，即原始绳段的长度，数字间以空格分隔。所有整数都不超过 $10^4$ 。

输出格式：

在一行中输出能够串成的绳子的最大长度。结果向下取整，即取为不超过最大长度的最近整数。

输入样例：

1
2

8
10 15 12 3 4 13 1 15

输出样例：

1

14

思路

一开始以为是huffman编码，其实不用那么麻烦。每次找到最小的两个结成新绳子（求平均）即可。

由于要从小到大来找绳子，当然排序是首先想到的方法。但是绳子的长度不超过10^4，所以既然最多的情况都要用int[10000]的数组，不如巧妙地用它来记录数量而不是长度，这样就不需要排序，时间复杂度为O(N)。

最短的绳子不需要和之前最短的绳子求平均，但如果设初值为最短绳子的长度，就没有这个特殊处理了，第一个for循环就是做这个。

看出来了，25分的题要不是考验数学能力的，就是间接考察数据结构和算法的。

代码

Github最新代码，欢迎交流

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include <stdio.h>

int main()
{
	int l[10001] = {0}, N, i;
	double length = 0;

	scanf("%d", &N);
	for (int j = 0; j < N; j++) {
		scanf("%d", &i);
		l[i]++;                 /* record counts */
	}

	for (i = 0; i < 10001; i++)  /* find the shortest, special case */
		if (l[i]) {
			length = i;
			break;
		}

	for (; i < 10001; i++)       /* make new ropes */
		while (l[i]--)
			length = (length + i) / 2;

	printf("%d", (int)length);

	return 0;
}